3.3_Security_对称密钥算法之AEAD

https://github.com/carloscn/blog/issues/145

3.3_Security_对称密钥算法之AEAD

简单的说，把3.0_Security_对称密钥算法加解密和3.2_Security_对称密钥算法之MAC（CMAC/HMAC）结合在一起，就是AEAD。全称为：Authenticated Encryption (AE) and Authenticated Encryption with Associated Data (AEAD)

对于AEAD的编程接口：

• 加密：

  • 输入：明文、密钥、header（未加密，可选）；

  • 输出：密文和MAC（tag）

• 解密：

  • 输入：密文，密钥，tag，header（在加密的时候使用的，可选）

  • 输出：明文，验证tag的结果，如果有header也有验证header的结果；

注意，header的目的是提供认证和完整性的保护，应用场景在网络和存储的metadata，是对不需要保证安全性但是需要认证功能的数据。

常用的AEAD包含：

• CCM

• ChaCha20-Poly1305

• CWC

• EAX

• GCM

• IAPM

• OCB

1. 安全背景

对称加密算法只能提供保密性，MAC只能提供认证的功能，如果想让两个结合，那么就需要人工的使用加密算法及MAC，这种组合是多种多样的，并没有一个完善的标准规定，而且易错(error prone)。大量的攻击可以侵入，由于加密+认证错误的实现。大概2000年的时候，Charanjit Jutla，这个人集成了CBC模式的加密与认证混合的工具IAPM mode。在2009年，又逐步的定义了6种认证加密模式：

• offset codebook mode 2.0, OCB 2.0;
• Key Wrap;
• counter with CBC-MAC CCM;
• encrypt then authenticate then translate, EAX;
• encrypt-then-MAC, EtM;
• Galois/counter mode, GCM)

在2013年，CAESAR competition 推行认证加密模式。在2015年，ChaCha20-Poly1305被加入到GCM中。

至此，一种又可以加密又可以保证完整性的算法工具诞生了。

2. AEAD

单纯的对称加密算法，其解密步骤是无法确认密钥是否正确的。也就是说，加密后的数据可以用任何密钥执行解密运算，得到一组疑似原始数据，而不知道密钥是否是正确的，也不知道解密出来的原始数据是否正确。因此，需要在单纯的加密算法之上，加上一层验证手段，来确认解密步骤是否正确。简单地把加密算法和认证算法组合，可以实现上述目的，并由此产生了几个方案：

• EtM (Encryption then MAC)

• E&M (Encryption and MAC)

• MtE (MAC then Encryption)

2.1 AEAD前身

2.1.1 (old) Encrypt-then-MAC (EtM)

先加密，然后对密文进行 MAC 运算（一般用各种 HMAC），把二者拼接起来，发给接收方。接收方先验证 MAC，如果验证通过，则证明密钥是正确的，然后执行解密运算。

参考： RFC-7366.

Various EtM ciphersuites exist for SSHv2 as well，(e.g., [e-mail]).

2.1.2 (old) Encrypt-and-MAC (E&M)

同时对原始数据执行加密和 MAC 运算，把二者拼接起来，发给接收方。接收方先进行解密，然后对解密结果执行 MAC 运算，比对发来的 MAC，验证正确性。

Used in, e.g., SSH

2.1.3 (old) MAC-then-Encrypt (MtE)

与 EtM 相反，先对原始数据执行 MAC 运算，与原始数据拼接后，执行加密算法，将密文发送给接收方。接受方先进行解密，然后执行 MAC 运算，验证解密结果是否正确。

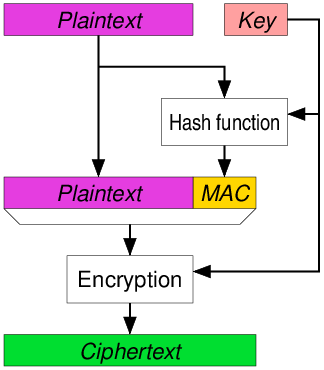
AEAD is used in SSL/TLS

2.2 AEAD

业内逐渐意识到以上通过组合加密和认证算法来实现 AEAD 的方案都是有安全问题的。从 2008 年起，业内开始提出，需要在一个算法在内部同时实现加密和认证。基于以上三个方法的思想，一些新的算法被提出，这些算法被称为真正的 AEAD 算法。

• AES-128-GCM

• AES-192-GCM

• AES-256-GCM

• ChaCha20-IETF-Poly1305

• XChaCha20-IETF-Poly1305

在具备 AES 加速的 CPU（桌面，服务器）上，建议使用 AES-XXX-GCM 系列，移动设备建议使用 ChaCha20-IETF-Poly1305 系列。在设计加密系统的时候，请务必选用 AEAD算法，抛弃旧的 MtE，EtM，E&M方案。

2.2.1 GCM

GCM原理

GCM 全称为 Galois/Counter Mode (GCM)，可以看出 G 是指 GMAC，C 是指 CTR。它在 CTR 加密的基础上增加 GMAC 的特性，解决了 CTR 不能对加密消息进行完整性校验的问题。

GCM 加密所需数据：明文 P、加密密钥 Key、初始向量 IV、附加消息 F。

GCM 加密步骤如下：

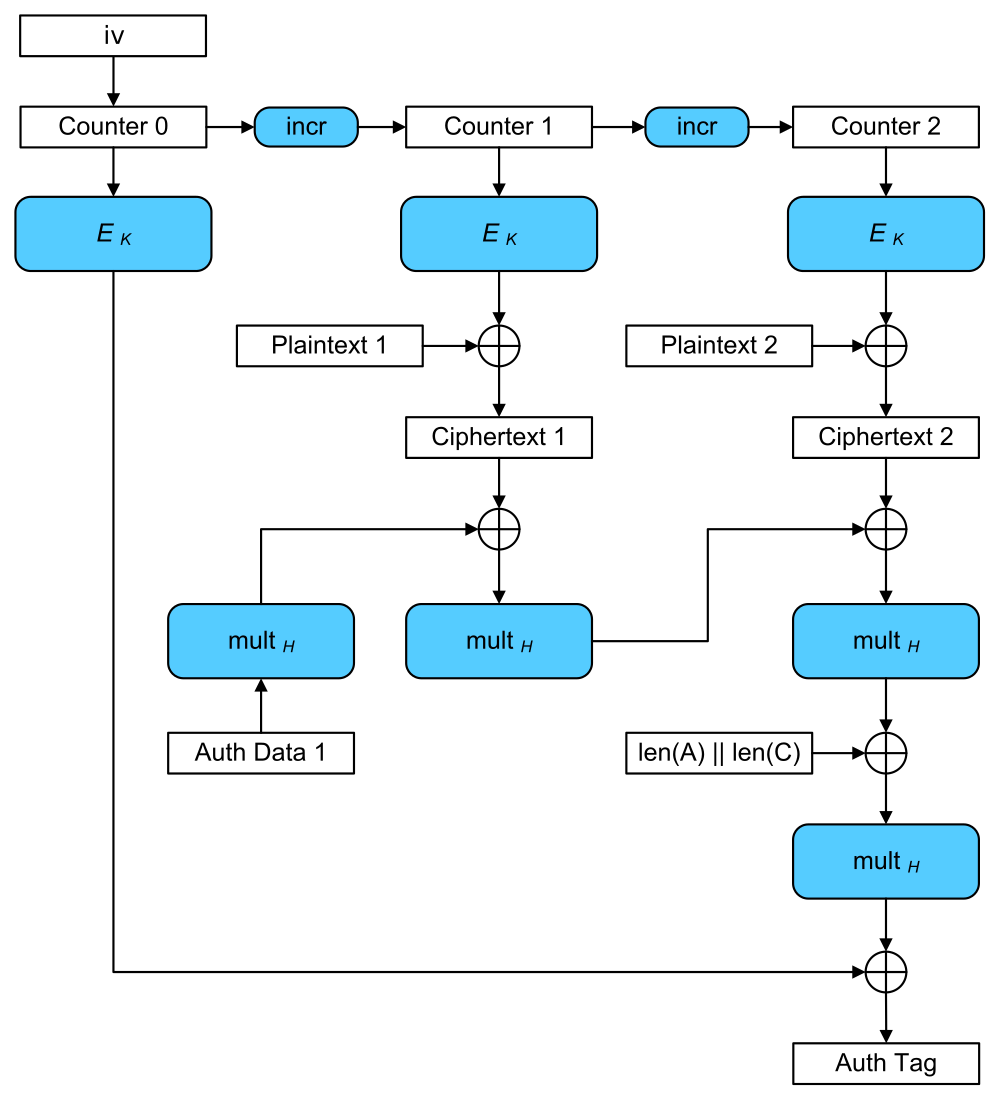
• 将 P 分为 P1、P2、…、Pn，Px 长度 <= 128

• 生成累加计数器 c0、c1、c2、…、cn，由密钥 Key 计算出密钥 H

• 将 IV、c0 进行运算（连接、加和、异或等）得到 IV_c0，用 Key 加密 IV_c0 得到 IVC0

• 将 IV、c1 进行运算（连接、加和、异或等）得到 IV_c1，用 Key 加密 IV_c1 得到 IVC1，将 IVC1、P1 做异或运算得到 C1，用密钥 H 通过 GMAC 算法将附加消息 F 计算出 F1， F1 与 C1 做异或运算得到 FC1

• 将 IV、c2 进行运算（连接、加和、异或等）得到 IV_c2，用 Key 加密 IV_c2 得到 IVC2，将 IVC2、P2 做异或运算得到 C2，用密钥 H 通过 GMAC 算法将附加消息 FC1 计算出 F2， F2 与 C2 做异或运算得到 FC2

• …

• 将 IV、cn 进行运算（连接、加和、异或等）得到 IV_cn，用 Key 加密 IV_cn 得到 IVCn，将 IVCn、Pn 做异或运算得到 Cn，用密钥 H 通过 GMAC 算法将附加消息 FC(n-1) 计算出 Fn， Fn 与 Cn 做异或运算得到 FCn

• 拼接 C1、…Cn 得到密文 C，用密钥 H 通过 GMAC 算法结合 FCn 和 IVC0 最终计算出 MAC

For any given key and initialization vector combination, GCM is limited to encrypting 239−256 bits of plain text (64 GiB)

参考：AES Galois Counter Mode (GCM) Cipher Suites for TLS

需要注意的是，GCM能够使用128/192/256的key长度，并且总以128bits作为块长度。 参考： https://crypto.stackexchange.com/questions/77750/why-gcm-operation-mode-with-aes-128-is-recomended-and-can-we-use-aes-192-and-aes

GCM mbedtls库

void setup() {
	  mbedtls_gcm_context aes;
	  char *key = "abcdefghijklmnop";
	  char *input = "Mark C's ESP32 GCM Example code!";
	  char *iv = "abababababababab";
	  unsigned char output[64] = {0};
	  unsigned char fin[64] = {0};
	  Serial.println("[i] Encrypted into buffer:");
	  
	  // init the context...
	  mbedtls_gcm_init( &aes );
	  // Set the key. This next line could have CAMELLIA or ARIA as our GCM mode cipher...
	  mbedtls_gcm_setkey( &aes,MBEDTLS_CIPHER_ID_AES , (const unsigned char*) key, strlen(key) * 8);
	  // Initialise the GCM cipher...
	  mbedtls_gcm_starts(&aes, MBEDTLS_GCM_ENCRYPT, (const unsigned char*)iv, strlen(iv),NULL, 0);
	  // Send the intialised cipher some data and store it...
	  mbedtls_gcm_update(&aes,strlen(input),(const unsigned char*)input, output);
	  // Free up the context.
	  mbedtls_gcm_free( &aes );
	  
	  for (int i = 0; i < strlen(input); i++) {  
	    char str[3];
	    sprintf(str, "%02x", (int)output[i]);
	    Serial.print(str);
	  }
	  
	  Serial.println("[i] Decrypted from buffer:");
	  mbedtls_gcm_init( &aes );
	  mbedtls_gcm_setkey( &aes,MBEDTLS_CIPHER_ID_AES , (const unsigned char*) key, strlen(key) * 8);
	  mbedtls_gcm_starts(&aes, MBEDTLS_GCM_DECRYPT, (const unsigned char*)iv, strlen(iv),NULL, 0);
	  mbedtls_gcm_update(&aes,64,(const unsigned char*)output, fin);
	  mbedtls_gcm_free( &aes );
}

参考： https://gist.github.com/unprovable/892a677d672990f46bca97194ae549bc

2.2.2 ChaCha20-IETF-Poly1305

ChaCha20-Poly1305是Google所采用的一种新式加密算法，性能强大，在CPU为精简指令集的ARM平台上尤为显著（ARM v8前效果较明显），在同等配置的手机中表现是AES的4倍（ARM v8之后加入了AES指令，所以在这些平台上的设备，AES方式反而比chacha20-Poly1305方式更快，性能更好），可减少加密解密所产生的数据量进而可以改善用户体验，减少等待时间，节省电池寿命等。谷歌选择了ChaCha20和伯恩斯坦的Poly1305消息认证码取代过去一直在互联网安全领域使用的基于OpenSSL的RC4密码，谷歌最初是为了保证能够在Android手机上的Chrome浏览器和谷歌网站间的HTTPS（TLS/SSL）通讯。在谷歌采用TLS不久后，ChaCha20和Poly1305均用在OpenSSH中的ChaCha20-Poly1305新算法中，这使得OpenSSH可能避免因编译时间对OpenSSL产生依赖。ChaCha20还用于OpenBSD（一种多平台类UNIX操作系统）中的RC4随机数生成器，在DragonFlyBSD中作为内核的伪随机数产生器（Cryptographically Secure Pseudo-Random Number Generator，简称CSPRNG）的子程序。

ChaCha20-Poly1305是由ChaCha20流密码和Poly1305消息认证码（MAC）结合的一种应用在互联网安全协议中的认证加密算法，由Google公司率先在Andriod移动平台中的Chrome中代替RC4使用。由于其算法精简、安全性强、兼容性强等特点，目前Google致力于全面将其在移动端推广。

Daniel J. Bernstein教授，德裔美籍数学家、密码学家、程序设计师。Eindhoven University of Technology的数学与计算机教授，设计了salsa、chacha等著名的流密码算法和Poly1305消息认证码，对国际密码学界影响深远。

参考： https://datatracker.ietf.org/doc/html/rfc8439

ChaCha20-IETF-Poly1305原理

chacha20 过程如下：

加密参数

输入：

输入项	长度(Bytes)	说明
key	32	共享秘钥
iv	12	干扰项，每次不同
AAD	N	关联数据
plaintext	N	待加密数据明文

输出：

输出项	长度(Bytes)	说明
ciphertext	N	加密后的密文，长度与原始明文一致
TAG	16	认证标签

解密参数

输入：

输入项	长度(Bytes)	说明
key	32	共享秘钥
iv	12	干扰项，每次不同
AAD	N	关联数据
ciphertext	N	待加密数据明文
TAG	16	认证标签

输出：

输出项	长度(Bytes)	说明
plaintext	N	原始明文
result	1	完整性检查结果（1成功，0失败）

代码示例

int chachapoly_test(void)
{
	/*  Key 共享秘钥 */
    unsigned char skey2[32] = {
    0x2e,0xff,0xe4,0x85,0x1e,0x23,0x72,0xef,
    0x5c,0x44,0x14,0x75,0x61,0xd8,0xf0,0xa3,
    0xde,0x91,0x09,0x00,0x24,0x03,0x51,0x3c,
    0xf2,0xf6,0x6d,0x16,0xbd,0x78,0xd2,0x63};

    int ret = 0;
    EVP_CIPHER_CTX* ctx = NULL;
    EVP_CIPHER_CTX* dctx = NULL;
	/*  干扰项 iv */
    unsigned char iv[12] = {
        0x00, 0x01, 0x02, 0x03, 0x04, 0x05, 0x06, 0x07, 0x08, 0x09, 0x0a, 0x0b
    };
	/*  外部关联数据 AAD */
    unsigned char aad[128] = 
    {0x06,0x07,0x08,0x09,0x0a,0x0b,0x0c,0x0d,0x0e,0x0f,0x10,0x11,0x12,0x13,0x14,0x15,
     0x16,0x17,0x18,0x19,0x1a,0x1b,0x1c,0x1d,0x1f,0x20,0x21,0x22,0x23,0x24,0x25,0x26,
     0x06,0x07,0x08,0x09,0x0a,0x0b,0x0c,0x0d,0x0e,0x0f,0x10,0x11,0x12,0x13,0x14,0x15,
     0x16,0x17,0x18,0x19,0x1a,0x1b,0x1c,0x1d,0x1f,0x20,0x21,0x22,0x23,0x24,0x25,0x26,
     0x06,0x07,0x08,0x09,0x0a,0x0b,0x0c,0x0d,0x0e,0x0f,0x10,0x11,0x12,0x13,0x14,0x15,
     0x16,0x17,0x18,0x19,0x1a,0x1b,0x1c,0x1d,0x1f,0x20,0x21,0x22,0x23,0x24,0x25,0x26,
     0x06,0x07,0x08,0x09,0x0a,0x0b,0x0c,0x0d,0x0e,0x0f,0x10,0x11,0x12,0x13,0x14,0x15,
     0x16,0x17,0x18,0x19,0x1a,0x1b,0x1c,0x1d,0x1f,0x20,0x21,0x22,0x23,0x24,0x25,0x26};
    unsigned char ciphertext[1024] = {0};
    unsigned char res[1024] = {0};
    
    /* 原始明文 plaintext */
    unsigned char msg[] = "0123456789abcdefghijklmnopqrstuvwxyz";
    ctx = EVP_CIPHER_CTX_new();

    ret = EVP_EncryptInit_ex(ctx, EVP_chacha20_poly1305(), NULL, skey2, iv);
    printf("EncryptInit ret: %d\n", ret);

    int outlen, finallen, reslen;
	/* 加密输入 ADD */
    ret = EVP_EncryptUpdate(ctx, NULL, &outlen, aad, 32);
    ret = EVP_EncryptUpdate(ctx, NULL, &outlen, aad+64, 32);
    printf("Ret: %d Update AAD len: %d\n", ret, outlen);
	/* 加密原始数据 */
    ret = EVP_EncryptUpdate(ctx, ciphertext, &outlen, msg, 37);
    printf("Ret: %d Update len: %u\n", ret, outlen);
    print_strhex(ciphertext, outlen);
    
    ret = EVP_EncryptFinal(ctx, ciphertext, &finallen);
    printf("Ret: %d Final len: %u\n", ret, finallen);
    outlen += finallen;
    //print_strhex(ciphertext, outlen);

    /* 生成认证标签TAG */
    unsigned char* tag_data = ciphertext + outlen;
    EVP_CIPHER_CTX_ctrl(ctx, EVP_CTRL_AEAD_GET_TAG, 16, tag_data);
    outlen += 16;
    print_strhex(ciphertext, outlen);



    dctx = EVP_CIPHER_CTX_new();
    //iv[0] = 0x0f;
    //skey2[0] = 0xff;
    //tag_data[0] = 0x01;
    //aad[0] = 0x01;
    ret = EVP_DecryptInit_ex(dctx, EVP_chacha20_poly1305(), NULL, skey2, iv);
    printf("DecryptInit ret: %d\n", ret);

    ret = EVP_CIPHER_CTX_ctrl(dctx, EVP_CTRL_GCM_SET_TAG, 16, tag_data);
    printf("Ret: %d CTX set TAG\n", ret);
    
    ret = EVP_DecryptUpdate(dctx, NULL, &reslen, aad, 32);
    ret = EVP_DecryptUpdate(dctx, NULL, &reslen, aad+64, 32);
    printf("Ret: %d Update AAD len: %d\n", ret, reslen);

    ret = EVP_DecryptUpdate(dctx, res, &reslen, ciphertext, outlen - 16);
    printf("Ret: %d DecryUpdate once len: %u\n", ret, reslen);
    int totallen = reslen;

    ret = EVP_DecryptFinal(dctx, res, &reslen);
    printf("Ret: %d DecryptFinal len: %u\n", ret, reslen);
    //reslen += finallen;

    //print_strhex(res, totallen);
    printf("%s\n", res);
}